Wallstreetgol

This article describes the formula syntax and usage of the Z.TEST function in Microsoft Excel.

• Microsoft Excel 2011
• Microsoft Excel 2011 For Mac P Value Chart

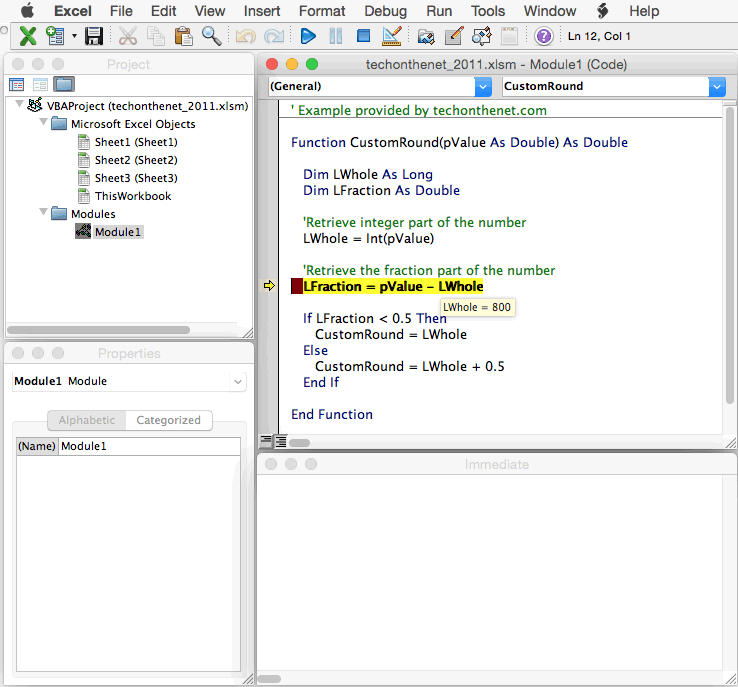
Returns the one-tailed P-value of a z-test.

Jan 21, 2017  A quick guide to obtain R2 (R squared) value from the linear regression model using Excel in Mac. The value returned by TTEST when tails=2 is double that returned when tails=1 and corresponds to the probability of a higher absolute value of the t-statistic under the “same population means” assumption. Copy the example data in the following table, and paste it in cell A1 of a new Excel worksheet.

For a given hypothesized population mean, x, Z.TEST returns the probability that the sample mean would be greater than the average of observations in the data set (array) — that is, the observed sample mean.

How do I display the number 0 in microsoft excel 2011? I wanted key in 0% but it displays as blank, can anyone help me with ms excel 2011 on how to make the 0% get displayed in the cells.

To see how Z.TEST can be used in a formula to compute a two-tailed probability value, see the Remarks section below.

Syntax

Z.TEST(array,x,[sigma])

The Z.TEST function syntax has the following arguments:

• Array Required. The array or range of data against which to test x.

• x Required. The value to test.

• Sigma Optional. The population (known) standard deviation. If omitted, the sample standard deviation is used.

Remarks

• If array is empty, Z.TEST returns the #N/A error value.

• Z.TEST is calculated as follows when sigma is not omitted:

  Z.TEST(array,x,sigma) = 1- Norm.S.Dist((Average(array)- x) / (sigma/√n),TRUE)

  or when sigma is omitted:

  Z.TEST(array,x) = 1- Norm.S.Dist((Average(array)- x) / (STDEV(array)/√n),TRUE)

  where x is the sample mean AVERAGE(array), and n is COUNT(array).

• Z.TEST represents the probability that the sample mean would be greater than the observed value AVERAGE(array), when the underlying population mean is μ0. From the symmetry of the Normal distribution, if AVERAGE(array) < x, Z.TEST will return a value greater than 0.5.

• The following Excel formula can be used to calculate the two-tailed probability that the sample mean would be further from x (in either direction) than AVERAGE(array), when the underlying population mean is x:

  =2 * MIN(Z.TEST(array,x,sigma), 1 - Z.TEST(array,x,sigma)).

Example

Microsoft Excel 2011

Copy the example data in the following table, and paste it in cell A1 of a new Excel worksheet. For formulas to show results, select them, press F2, and then press Enter. If you need to, you can adjust the column widths to see all the data.

Microsoft Excel 2011 For Mac P Value Chart